卡尔曼滤波(Kalman filtering)是一种利用线性系统 状态方程,通过系统输入输出观测数据,对系统状态 进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波 过程。
数据滤波是去除噪声 还原真实数据的一种数据处理 技术,Kalman滤波在测量方差已知的情况下能够从一系列存在测量噪声的数据中,估计动态系统的状态。(百度百科)
实际应用中,我们陀螺仪实验的时候,会发现获取的数值抖动太大,不够平滑;这样的数值在应用时会导致很多问题,因此需要通过一定的算法将数值转换的更平滑。如下采集数据:
105.87231557, 108.0076993, 85.64052734, 84.23328308, 124.71488794, 102.91086635, 96.6229862, 93.07739765, 98.52594135, 111.79610743, 94.78393208, 105.27301268, 87.23224952, 89.71036819, 117.43724425, 64.70525616, 75.48832499, 91.99249324, 105.44355624, 84.93538347
上面的数据是获取的陀螺仪Roll方向20次样本数据,可见数值波动很大,如84都124,89到117等。下面我们将尝试卡尔曼算法,实现数值降噪滤波。
代码示例:
#!/usr/bin/env python
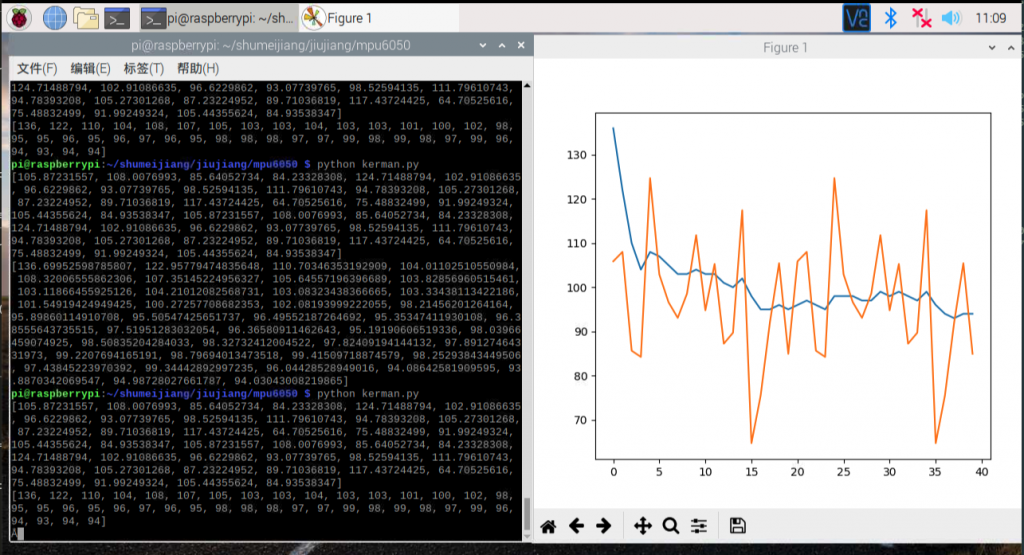
效果如图:
执行效果 上图可见,我们通过vnc进入可视化桌面,然后命令行执行程序文件,左侧是输出的数据;右侧是图表化滤波数据和原值数据,蓝色是滤波后数据,黄色是原值数据。可见,滤波后数据变的平滑很多。
算法部分来源于大神文章:https://blog.csdn.net/moge19/article/details/82531119
图形化展示部分,使用的是matplotlib,Python的2D绘图库;系统默认是没有安装的,需要自己安装,由于默认安装的matplotlib版本执行一直有问题,所以安装时指定了版本:
pip install matplotlib==2.0.2
安装后执行如果报问题:Couldn't find foreign struct converter for 'cairo.Context',那么执行如下命令:
sudo apt-get install python-gi-cairo
其他滤波算法,还没尝试,如果有兴趣可以试一下:十种滤波算法的Python实现。